En su versión más sencilla, el armonógrafo está formado por dos péndulos, dispuestos de manera que uno se mueve perpendicularmente a otro. Uno de los péndulos lleva acoplado un lápiz o cualquier otro útil de escritura y se encarga de moverlo, digamos, de adelante a atrás. El otro péndulo sirve para desplazar, en este caso de izquierda a derecha, la superficie sobre la que se dibuja; una hoja de papel o una cartulina, por ejemplo. El efecto combinado de los dos péndulos genera un movimiento que dibuja sobre el papel una curva. Jugando con la relación de frecuencias y el desfase entre ambos péndulos, la curva en cuestión puede ser completamente diferente: desde algunas tan simples como circunferencias y elipses hasta otras figuras más complejas tales como las llamadas curvas de Lissajous. En condiciones ideales, el movimiento oscilatorio se mantendría hasta que alguna fuerza externa detuviese el vaivén de los péndulos. La gracia está en que, debido al rozamiento con el aire y con el papel, los péndulos se van frenando poco a poco. Cada nueva trazada del lápiz se encuentra muy próxima a la anterior y el resultado va adquiriendo una apariencia ondulatoria, como una especie de tela de araña, hasta que finalmente la trayectoria del lápiz se reduce a un único punto y se detiene.
El sonido hecho forma
Para explicar los orígenes del armonógrafo hay que contar la historia de un matemático francés que vivió durante el siglo XIX: Jules Antoine Lissajous (¿será el mismo Lissajous de las curvas que aparecieron antes?). Nacido en Versalles en 1822, Lissajous entró en la École Normale Supérieure en 1841 y apenas seis años después ya era profesor de matemáticas del Lycee Saint-Louis de París.
 |
| Louis Antoine Lissajous (1822-1880) |
Lissajous cogió un diapasón y colocó en su extremo un pequeño espejo. Entonces apuntó con un rayo de luz a dicho espejo, de forma que al reflejarse el rayo llegase a una pantalla oscura. De esta manera tan sencilla, la vibración del diapasón podía visualizarse en la pantalla. Lissajous comprobó que, cuando golpeaba el diapasón, aparecía en la pantalla una onda sinusoidal, cuya forma dependía de la frecuencia de vibración del diapasón.
No contento con esto, Lissajous fue un paso más allá y modificó este esquema. En vez de un único diapasón, añadió a su experimento otro más, colocado en ángulo recto con respecto al primero, y con su correspondiente espejo en el extremo. Luego dispuso el conjunto de forma que un rayo de luz se reflejase, sucesivamente, en ambos espejos antes de proyectarse sobre la pantalla. Ahora el patrón que vio en la pantalla no tenía forma sinusoidal: era más complejo y dependía de la relación simple entre las frecuencias de vibración de ambos diapasones.
 |
| Esquema del experimento de Lissajous. |
El trabajo de Lissajous fue elogiado por sus contemporáneos y su método fue exhibido en la Exposición Universal de París de 1867. Seis años después recibió el prestigioso Premio Lacaze por sus “hermosos experimentos”. Fue algo más que eso, puesto que su método se considera un precursor del moderno osciloscopio. Desde entonces, las figuras que se obtienen se conocen en su honor como curvas de Lissajous.
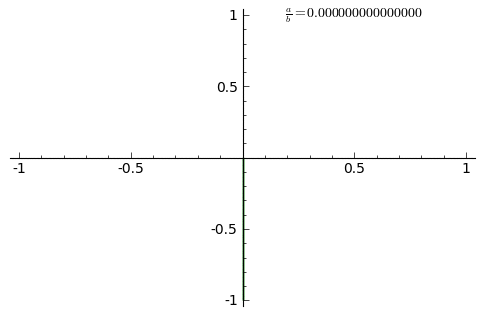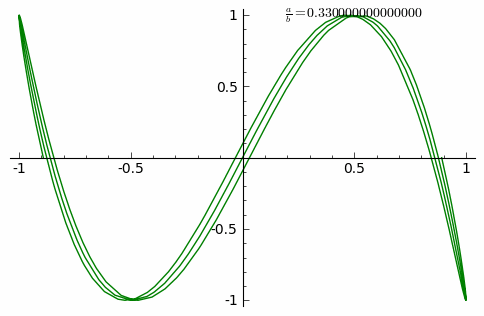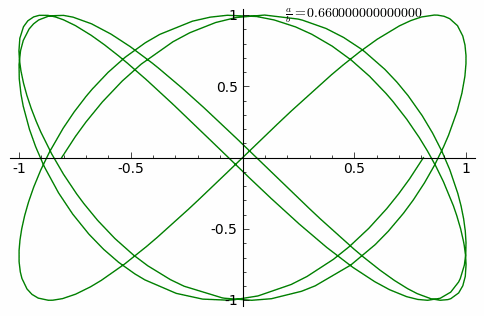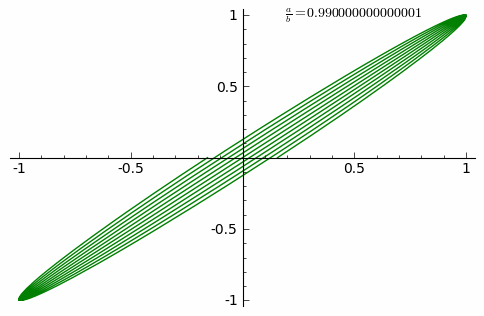 |
| Esta animación muestra las distintas curvas de Lissajous cuando la relación (a/b) entre las frecuencias de los péndulos aumenta en intervalos de 0,01 hasta 1. |
El péndulo de Bowditch
Lo más curioso de esta historia es que Lissajous no fue el primero en estudiar este tipo de curvas. En 1815, un capitán de navío y científico autodidacta llamado Nathaniel Bowditch (1773-1838) también estaba interesado en el movimiento ondulatorio y publicó sus conclusiones en un artículo de la revista de la American Academy of Arts and Science. Pero no recurrió a diapasones y espejos, como haría después Lissajous, sino que se limitó a utilizar el objeto oscilatorio por antonomasia: el péndulo.
 |
| Péndulo suspendido de dos hilos con sus dos planos de oscilación. |
Este péndulo así construido tenía dos modos de oscilación distintos. En el primero de ellos, la pelota oscilaba en el plano perpendicular a la "Y", y lo hacía pivotando sobre los dos puntos fijos al tablero. El otro modo consistía en el movimiento del péndulo en el mismo plano de la "Y". Pero ahora el péndulo no oscilaba sobre los dos puntos de arriba, sino que lo hacía, para entendernos, sobre el vértice de la "V". En ambos casos, el movimiento era equivalente al de un péndulo simple, sólo que la longitud efectiva del péndulo variaba en cada uno.
Cuando el péndulo oscilaba en una de estas dos direcciones, el resultado no tenía nada de especial. Pero, ¿y si lo hacía en una dirección oblicua? Bodwitch se dio cuenta que entonces el movimiento se complicaba. Unas veces el péndulo trazaba una trayectoria circular; en otras ocasiones, era elíptica, parabólica o describía una curva con dos ramas, parecido a un ocho. Incluso a veces, el movimiento del péndulo describía todas ellas de forma cíclica. Bodwitch comprendió que había una inmensa variedad de estas curvas o de combinaciones de ellas, y que dependían de las proporciones que las diferentes partes del péndulo mantuviesen entre sí: básicamente, la longitud de las cuerdas que formaban la "Y". La variación de estas magnitudes producía cambios en las formas de las curvas.
Primeros armonógrafos
El caso es que la historia parece haberse olvidado de Bowditch y su péndulo suspendido de dos puntos, así que vamos a dar otro salto en el tiempo hasta el último cuarto del siglo XIX. Fue entonces cuando se empezaron a construir los primeros armonógrafos como una manera de analizar las vibraciones y, en concreto, para estudiar el sonido, de forma análoga a como lo había hecho Lissajous. (Precisamente de ahí viene el nombre de armonógrafo, “que dibuja la armonía”. Por eso en español se escribe sin h, mientras que en inglés se escribe con h, del equivalente harmony.) Estos armonógrafos seguían el esquema de Lissajous, pero enseguida surgieron otros que cambiaban el movimiento ondulatorio de la luz por el de un péndulo, tal y como se explicaba al principio de la entrada. Las demostraciones de este tipo de instrumentos fascinaron tanto al público que su uso se multiplicó, convirtiéndose en un pasatiempo muy extendido. Las damas victorianas se reunían alrededor de los armonógrafos a conversar mientras éstos dibujaban sus hermosos patrones. Una tienda de Londres se dedicaba a vender modelos portátiles que se podían guardar en un maletín y llevarse cómodamente para amenizar cualquier fiesta. A finales del siglo XIX, el armonógrafo estaba de moda.
 |
| Armonógrafo de Messrs Newton & co, 1909. (Crédito: Science Museum / Science & Society Picture Library) |
Al mismo tiempo que se extendió su uso, también se complicó su diseño para producir dibujos aún más bellos. El armonógrafo que hemos visto antes se conoce como armonógrafo lateral, por el movimiento de sus dos péndulos, que se desplaza uno con respecto al otro lateralmente. Existen otro tipo de aparato que incorpora un tercer péndulo y que se llama armonógrafo rotatorio. En este caso, dos péndulos oscilan en ángulos rectos como antes, pero ahora ambos están unidos al lápiz mediante un par de brazos y normalmente se ajustan para que su movimiento combinado sea circular. Justo debajo del lápiz, el tercer péndulo está montado sobre un cojinete rotatorio, lo que permite que la tabla acoplada a este péndulo describa otro círculo. Al bajar el lápiz, ambos movimientos se combinan sobre el papel. Dependiendo de que el sentido de giro sea el mismo u opuesto, la combinación de estos movimientos pendulares producen dibujos de muy distinta factura.
Ajustes
Supongamos que cae en tus manos un armonógrafo y que quieres entretenerte con él. ¿Cómo ajustarlo? Lo primero que hay que saber es que el tiempo que tarda un péndulo en realizar una oscilación sólo depende de la longitud del péndulo, y no de su peso ni del arco que recorre al oscilar. Éste es el principio básico del péndulo, tal y como lo estableciera Galileo Galilei hace más de cuatrocientos años.
El tiempo que tarda un péndulo en oscilar está relacionado con una magnitud muy habitual en física que es la frecuencia, el número de oscilaciones por segundo. Cuanto mayor sea la longitud del péndulo, más tiempo tardará en realizar una oscilación y, por tanto, menor será su frecuencia. (En concreto, la frecuencia de un péndulo varía inversamente con la raíz cuadrada de la longitud del péndulo. Es decir, que para triplicar la frecuencia de un péndulo, debemos reducir su longitud a la novena parte.) Los armonógrafos suelen llevar unas fijaciones para variar la altura del peso de cada péndulo, lo que acorta o alarga su longitud y permite cambiar su frecuencia de oscilación. Lo normal es que si uno ajusta de cualquier manera las frecuencias de los péndulos, el resultado sea un movimiento errático y el dibujo del armonógrafo, caótico. Sólo cuando la relación entre las frecuencias de los péndulos sea una fracción de números naturales, surgirán curvas reconocibles. (Es un buen momento para recordar la analogía entre el armonógrafo y la música. La unión de dos sonidos cualesquiera no produce en general un sonido agradable. Sin embargo, si las frecuencias de esos dos sonidos son proporcionales entre sí o bien una fracción simple de ellas, entonces el sonido es armónico.) Por ejemplo, en el caso del armonógrafo lateral, cuando las frecuencias de los dos péndulos son iguales (diríamos entonces que la relación es 1:1), el dibujo resultante es una recta, una circunferencia o una elipse, dependiendo del desfase entre los dos péndulos. Puedes comprobarlo en este simulador de armonógrafo.
Una vez conseguido un movimiento armónico de los péndulos, resulta muy interesante realizar pequeñas variaciones de las frecuencias a partir de esos valores. De esta manera se pueden conseguir dibujos realmente sorprendentes. Fíjate lo que ocurre cuando hacemos algo así con la imagen anterior.
Otra variable a tener en cuenta para ajustar el movimiento del armonógrafo es el peso del péndulo. Esto no va alterar la frecuencia del péndulo, pero sí va a influir en el rozamiento: cuanto mayor sea el peso del péndulo, menor será la fricción con el aire, las bisagras y el papel. Si el péndulo se detiene muy pronto, se puede aumentar su peso para que tarde más en pararse. En cambio, si el movimiento del péndulo es demasiado alegre, se le puede quitar peso para ralentizarlo.
Esto es básicamente lo que hay que saber para manejar un armonógrafo. El resto es cuestión de que construyas uno y te pongas a experimentar. Puedes encontrar en Internet muchos vídeos y páginas con las instrucciones de cómo hacerlo. No me resisto a poner este vídeo donde se describe de forma muy clara (eso sí, en inglés) un armonógrafo ¡de cuatro péndulos! Una maravilla...
Pero el armonógrafo puede resultar algo más que un simple entretenimiento. Que se lo pregunten si no al diseñador sueco Eske Rex, que lo utiliza habitualmente en su trabajo. Aquí hay algunas imágenes del resultado, aunque lo mejor es que veas el vídeo de su imponente armonógrafo en acción:
En definitiva, hay muchas razones para tener tu propio armonógrafo, si tienes tiempo, cierta habilidad manual y espacio para colocarlo. Aquí te dejo algunas más, por si no te he convencido:
¿Te animas?
NOTA: Esta entrada participa en la Edición 2.6 del Carnaval de Matemáticas que alberga La Vaca Esférica. También participa en la XXIII Edición del Carnaval de la Física que organiza Astrofísica y Física.
NOTA: Esta entrada participa en la Edición 2.6 del Carnaval de Matemáticas que alberga La Vaca Esférica. También participa en la XXIII Edición del Carnaval de la Física que organiza Astrofísica y Física.
REFERENCIAS:
- Anthony Ashton, Harmonograph: a visual guide to the mathematics of music. Walker & Company, 2003.
- Clifford A. Pickover, The Math Book. Sterling, 2009.
- Nathaniel Bodwitch, On the motion of a pendulum suspended from two points. American Academy of Arts and Science, septiembre 1815.
Todas las imágenes son de dominio público salvo donde se indique lo contrario.









Yo quiero uno!
ResponderEliminarYo vendo uno
Eliminarhuevos tu fantastico, fantastica mi verga
ResponderEliminaryo quiero a tu mama y a tu hermana y no te lo ando diciendo
ResponderEliminar