Estaba barajando varios temas para mi participación en la Edición 2.7 del Carnaval de Matemáticas. Como he visto que hay un par de entradas sobre paradojas, y dicen que no hay dos sin tres, ahí va la mía. Se trata de responder a la siguiente pregunta: ¿se puede pintar una superficie infinita con un bote de pintura?
En principio, la respuesta intuitiva es que no. Para pintar una superficie infinita se necesitaría un bote de pintura infinitamente grande. Pero en matemáticas no basta con la intuición, las cosas hay que demostrarlas. Vamos allá.
Consideremos la función f(x)=1/x, una curva muy familiar que seguro que has visto representada alguna vez.
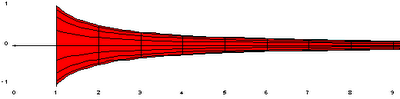
Nos vamos a centrar en el intervalo de x entre 1 e infinito y vamos a hacer girar esa curva alrededor del eje de abcisas, tal y como muestra la siguiente imagen.
El resultado tendría aspecto de trompeta; una especie de vuvuzela infinitamente larga. ¿Que no lo acabas de ver claro? Seguro que esta imagen en 3-D te ayuda.
¿Cuál es la superficie de este objeto? Cualquier estudiante de ciencias puede resolver la integral correspondiente y obtener que, así construido, este objeto tiene una superficie infinita. ¿Y su volumen? Si tiene una superficie infinita, debería tener un volumen infinito. Pero de nuevo, no basta con aplicar la intuición, hay que calcularlo. Y ahora viene lo bueno. Cuando uno realiza el cálculo, resulta que el volumen de este objeto ¡es p! Se trata, por tanto, de un objeto con una superficie infinita pero con un volumen finito.
Este objeto se conoce como la trompeta de Torricelli, y debe su nombre al físico y matemático italiano Evangelista Torricelli (1620-1675). Aunque en la actualidad se le recuerda por la invención del barómetro de mercurio y por ser el discípulo aventajado de Galileo, Torricelli fue un matemático de considerable talento. En 1641 descubrió este objeto matemático que le dejó perplejo: un sólido geométrico que es infinitamente largo, pero que tiene un volumen finito. (Recordemos que entonces no se había desarrollado todavía el cálculo como herramienta matemática, así que llegar a este resultado ya tiene su mérito.) Torricelli comunicó su descubrimiento a los geómetras franceses en cartas escritas en 1644. El resultado parecía tan contraintuitivo y sorprendente que al principio algunos de los matemáticos europeos más destacados pensaron que no era posible, como lo podría pensar cualquier profano en la materia. Las matemáticas siempre pueden sorprenderte, por muy experto que seas.
Volvamos ahora a la pregunta inicial. Si tiene una superficie infinita, nunca se podría pintar su cara interior con un bote de pintura. Sin embargo, al tener un volumen finito, se puede introducir una cierta cantidad de pintura con la que llenar el embudo de la trompeta de Torricelli. Y si se llena el embudo esto significa que has pintado la cara interior, que acabamos de decir que es infinita. Ahí está la paradoja.
¿Sorprendente, verdad? Pues realmente esta paradoja no es tal. Primero, porque esto no deja de ser un objeto matemático; no se puede construir en la realidad una trompeta infinitamente larga. Y segundo, aunque se llenase de pintura la trompeta, no se pintaría toda su superficie interna. Al hacerse infinitamente estrecha, llegaría un momento que las moléculas de la pintura no podrían avanzar. En otras palabras, el diámetro de la trompeta sería más pequeño que el diámetro de una molécula de pintura, por lo que no se cubriría el resto de la superficie de la trompeta.
La trompeta de Torricelli también se conoce en ocasiones como el cuerno de Gabriel. Este nombre sugiere la imagen del Arcángel Gabriel haciendo sonar su cuerno para anunciar el día del Juicio Final, asociando así el infinito, los poderes de Dios, con lo finito, el mundo terrenal.